Binomial_MetaBacktest.ex4 Binomial_MetaBacktest.mq4 EURUSD-M1-Setting.set
Report-Binomial-Distribution-EURUSD-M1.zip
Home / Articles / #11
How to Build a Probability-Aware EMA Trading Strategy Using the Binomial Distribution in MQL4 with MetaBacktest
Hadi
2025-10-15 08:42:39
In quantitative trading, strategies that combine technical indicators with statistical reasoning often outperform purely signal-driven systems. While many MetaTrader 4 (MQL4) traders rely on exponential moving averages (EMAs) for directional bias, few integrate probabilistic confidence models to adapt their position sizing dynamically.
This article explores a simple yet powerful approach:
- A traditional EMA crossover system for trade direction
- Fixed stop loss (SL) and take profit (TP) for clear binary outcomes
- A Binomial distribution model that statistically evaluates the previous
ntrades - An adaptive lot-sizing mechanism that increases exposure when probability outcomes suggest statistical edge
All of this is done purely in MQL4, no external languages or libraries — simple, efficient, and fully deployable on MT4.
Deep-dive notes (explanations, caveats & tuning)
-
How the binomial decision is made
-
Two modes:
-
UsePValueMethod = true: compute , where is the number of wins in the lastLookbackNtrades and (p_0` is a null probability (default 0.5). If this survival probability is ≥ DecisionThresholdP (default 0.70), we treat the recent window as “good” and increase next lot.-
Interpretation: observing at least
Wwins is relatively likely under the assumption of p_0. This is a heuristic — you can tune p0 and the threshold to be conservative or aggressive.
-
-
UsePValueMethod = false: compute Beta posterior mean and compare toPosteriorThreshold. This smooths the estimate for small N and avoids extreme swings.BetaAlphaPrior/BetaBetaPriordefault to 1 (uniform).
-
-
Both are heuristics for adaptive sizing. You can easily swap or add more sophisticated logic (e.g., require both tests to pass).
-
-
Why a sliding window of closed trades (LookbackN)?
-
It gives a recent performance snapshot. Choose
LookbackNas a tradeoff: small N reacts quickly but is noisy; large N is stable but slow to react. Typical values: 20–100 depending on trade frequency.
-
-
What counts as a 'win'?
-
In this EA, a closed trade with total profit (profit + swap + commission) ≥ 0 is considered a win. You can change this criterion (e.g., require profit >= some positive threshold or use net returns percent).
-
-
Lot sizing policy
-
This EA resets to
BaseLotwhen the binomial test is not satisfied, and multiplies byLotMultiplierwhengood. Alternative strategies:-
Gradual increase (increment rather than multiply).
-
Add decay (reduce lot gradually rather than full reset).
-
Cap total exposure by
MaxOpenTradesandMaxLot— both included.
-
-
-
Numerical stability & PMF
-
PMF uses recurrence and computes tail sums via
BinomialSurvivalwhich sums the smaller tail for numerical stability. This is robust forLookbackNup to hundreds/thousands with double precision. If you use extremely large windows (e.g., >10k), switch to log-domain or normal approximation.
-
-
How closed-trades are processed
-
The EA marks all history tickets present at
OnInitas processed (so restarting the EA doesn't retroactively change sizing based on old data). It only processes newly closed trades after it starts. If you want to include historical trades for quicker bootstrap, remove or change that block inOnInit.
-
-
Risk management
-
This EA is a demo of binomial-based sizing. In live systems ensure:
-
Maximum drawdown protections,
-
Overall portfolio exposure caps,
-
Equity/loss-based stop triggers,
-
Proper money management (Kelly-based or volatility sizing) if required.
-
-
-
Backtest & validation
-
Backtest to measure how quickly the system reacts to changing win rates and its effect on drawdown/returns.
-
Unit tests to verify
BinomialPMFArraysums to ~1, mean ~ n*p, survival matches direct sums for small n.
-
-
Extending the decision rule
-
Replace the simple multiplier with a sizing function that maps posterior mean (or p-value) into a continuous lot factor, e.g.
lot = base * (1 + k*(postMean - 0.5))clipped to[min, max].
-
-
Practical tuning suggestions
-
Conservative: LookbackN=50, DecisionP0=0.5, DecisionThresholdP=0.9, LotMultiplier=1.5
-
Aggressive: LookbackN=20, DecisionP0=0.5, DecisionThresholdP=0.65, LotMultiplier=2.0
-
-
W= number of wins -
L= number of losses = n - W -
p̂= W / n (the empirical probability of winning) -
If your recent 20 trades yielded 15 wins (p̂ = 0.75),
-
The probability of achieving ≥15 wins by random chance (assuming a neutral 0.5 win rate) can be computed via the Binomial tail probability.
-
Mathematically grounded: uses the binomial model to measure confidence
-
Emotion-free scaling: increases or decreases lot size only when statistically justified
-
Self-adaptive: responds automatically to market regime shifts
-
Simple structure: easy to backtest, extend, and deploy
-
Keep
HistoryTradesbetween 20–50 for short-term learning. -
Use fixed SL/TP to maintain binary outcomes.
-
Update the binomial probability after each closed trade.
-
Integrate
BinomialTail()checks into your performance analytics dashboard. -
For large-scale systems, you can approximate using a normal approximation to save computation.
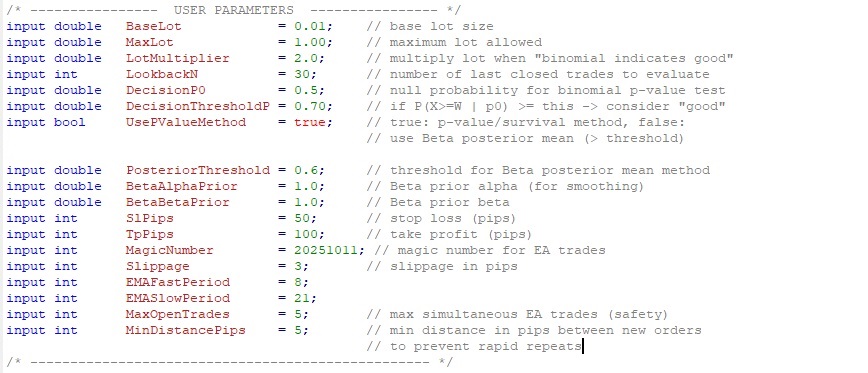
- Instrument : EURUSD
- Timeframe : 01
- Period : Jan 2012 – Aug 2025
- base lot size : 0.01
- maximum lot allowed : 1.0
- multiply lot when "binomial indicates good" : 2.0
- number of last closed trades to evaluate : 30
- null probability for binomial p-value test : 0.5
- if P(X>=W | p0) >= this -> consider "good" : 0.002
- true: p-value/survival method : True
- threshold for Beta posterior mean method : 0.6
- Beta prior alpha : 1.0
- Beta prior beta : 1.0
- stop loss (pips) : 150
- take profit (pips) : 15
- slippag in pips : 3
- EMAFastPeriod : 8
- EMASlowPeriod : 21
- max simultaneous EA trades : 1
- min distance in pips between new orders : 5
Encoding Outcomes for Statistical Learning
After n trades, we can compute:
With this empirical win probability, we can model the sequence of outcomes using the Binomial distribution:
This gives the probability of achieving k wins out of n trades given your observed success rate.
* Download the EA from the Download Box HERE
The Role of the Binomial Distribution in Trading Adaptation
The Binomial distribution offers a statistical measure of confidence in your trading performance.
It tells you whether your recent success is likely random noise or a genuine statistical edge.
For example:
If this probability is low, it means your performance is unlikely due to chance — a potential real edge.
If it’s high, recent success may be random fluctuation — so you avoid overconfidence.
Thus, we can design a dynamic lot-sizing rule:
| Statistical Confidence | Trading Action |
|---|---|
| Strong (e.g., P < 0.05) | Increase lot size by small factor |
| Neutral (0.05 < P < 0.2) | Maintain current lot size |
| Weak (P > 0.2) | Reduce lot size to preserve capital |
Implementation in MQL4
Below is a simplified yet fully functional version of this logic.
It uses EMA8/EMA21 signals, tracks trade outcomes, and adapts lot size using a Binomial-based confidence test.
Why This Approach Matters
This trading framework doesn’t rely on magical parameters or curve-fitting.
It’s a systematic method for adjusting trade exposure based on quantified evidence of an edge.
Advantages:
Practical Recommendations
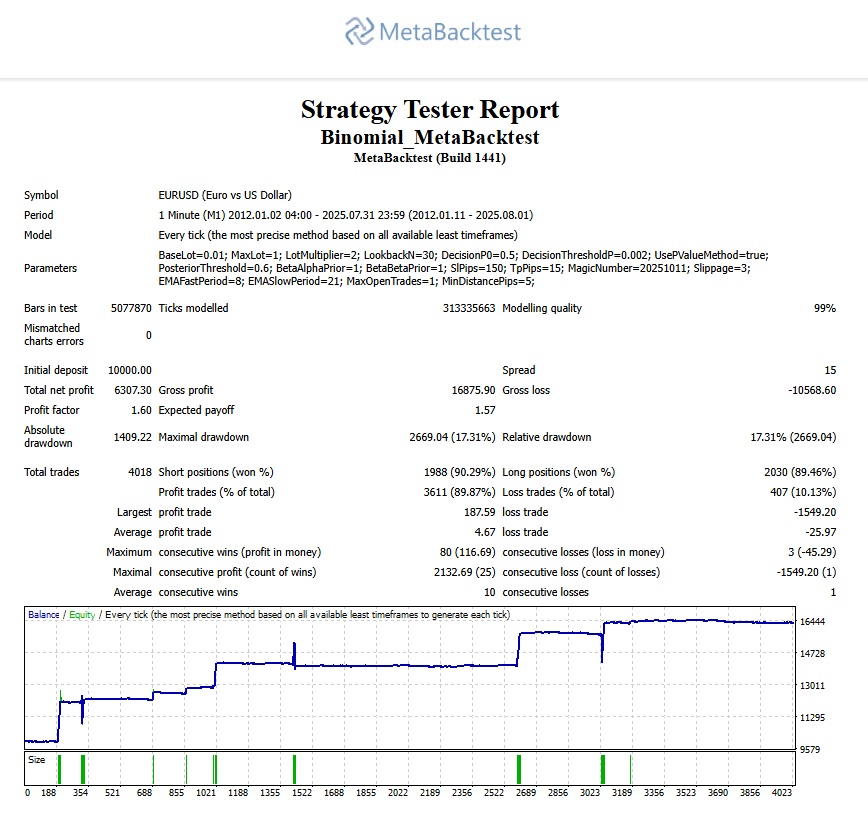
Backtest Results by MetaBacktest
We ran multiple backtests of the MQL4 Expert Advisor using MetaBacktest to ensure fair and transparent results.
Test Parameters:
* You can download the EA and setting file from the Download Box HERE
Process time: 39:49:45.672

Key Results:
Conclusion
Integrating the Binomial distribution into a trading system bridges the gap between signal-based logic and statistical validation.
By pairing a simple EMA crossover with binomial confidence, traders gain a dynamic, evidence-based mechanism for risk scaling — entirely within MQL4.
This method embodies the philosophy of MetaBacktest.com:
“Backtesting is not just about finding signals — it’s about validating probability.”
Does the MACD Zero Line Strategy Work? Backtest Results Revealed
2025-09-05 15:41:11
Backtesting the Evening Star & Morning Star Patterns with MetaBacktest
2025-10-03 12:42:09
How to Build a Probability-Aware EMA Trading Strategy Using the Binomial Distribution in MQL4 with MetaBacktest
2025-10-15 08:42:39
For the binomial test: using p0 = 0.5 is okay, but wouldn’t a custom prior (say 0.55) calibrated to your strategy be stronger?
Yup. Using beta priors or empirical p0 might boost responsiveness.
The binomial sizing logic is quite clever. But what if the strategy’s win rate shifts over time, won’t old trades bias the decision?
That’s why smoothing or a decayed weighting (more weight to recent trades) might help.